[알고리즘] #Maximum Depth of N-ary Tree

출처 :https://leetcode.com/problems/maximum-depth-of-n-ary-tree/

Maximum Depth of N-ary Tree - LeetCode

 

문제

Given a n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

For example, given a 3-ary tree:

 

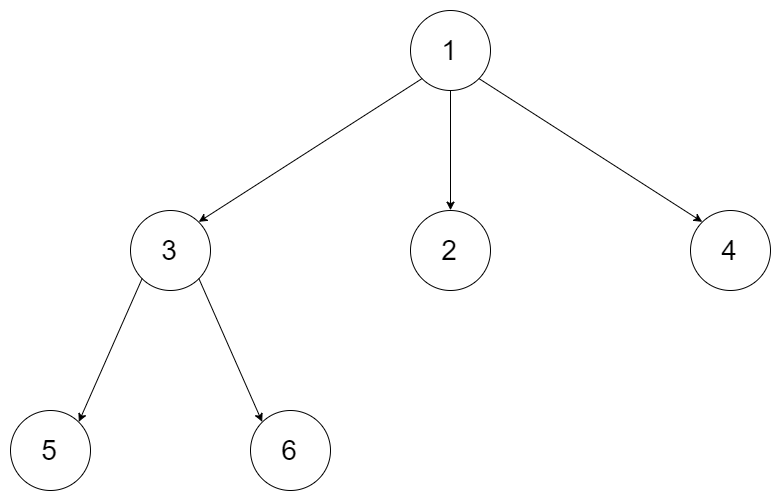
We should return its max depth, which is 3.

 

Note:

1. The depth of the tree is at most 1000.
2. The total number of nodes is at most 5000.

 

---

풀이

 

이 문제를 보자마자 지난 번에 풀었던 'Maximum Depth of Binary Tree' 가 떠올랐다. 지난 번에 풀었던 문제는 이진 트리였다면, 이번에 풀어야할 문제는 n-ary 트리이다. n-ary 트리는 자식 노드의 갯수가 n개 이하인 트리를 말한다.

이 문제도 지난번처럼 루트노드의 모든 자식 노드들을 방문해서 해당 노드들을 Stack에 넣은 뒤, depth를 계산하면 된다.

 

/**
 * // Definition for a Node.
 * function Node(val,children) {
 *    this.val = val;
 *    this.children = children;
 * };
 */
/**
 * @param {Node} root
 * @return {number}
 */
var maxDepth = function(root) {
    if(!root || !root.children) {
        return 0;
    }
    
    root.depth = 1;
    var max = getMaxDepth(root, 1);
    
    return max;
};

function getMaxDepth(node, max) {
    if(!node || !node.children) {
        return max;
    }
    
    if(node.children.length > 0) {
        if(node.depth > max) {
            max = node.depth;
        }
        
        var child = node.children;
        for(var i=0; i<child.length; i++) {
            child[i].depth = node.depth+1;
            if(max < child[i].depth) {
                max = child[i].depth;
            }
            max = getMaxDepth(child[i], max);
        }
    }
        
    return max;
}

 

 

 

 

 

 

 

참고 : https://gogomalibu.tistory.com/47

[알고리즘] #Maximum Depth of Binary Tree